Moscow, Russian Federation
VAK Russia 1.5.5
VAK Russia 1.5.8
VAK Russia 5.8.4
VAK Russia 5.8.5
VAK Russia 5.6.6
UDC 796.015
UDC 796.058.2
CSCSTI 77.00
CSCSTI 20.00
Russian Classification of Professions by Education 02.00.00
Russian Classification of Professions by Education 06.00.00
Russian Library and Bibliographic Classification 1
Russian Library and Bibliographic Classification 22
Russian Library and Bibliographic Classification 28
Russian Library and Bibliographic Classification 75
BISAC COM072000 Computer Simulation
BISAC COM017000 Cybernetics
BISAC COM062000 Data Modeling & Design
BISAC COM089000 Data Visualization
BISAC SPO047000 Training
BISAC BIO016000 Sports
BISAC MAT007010 Differential Equations / Ordinary
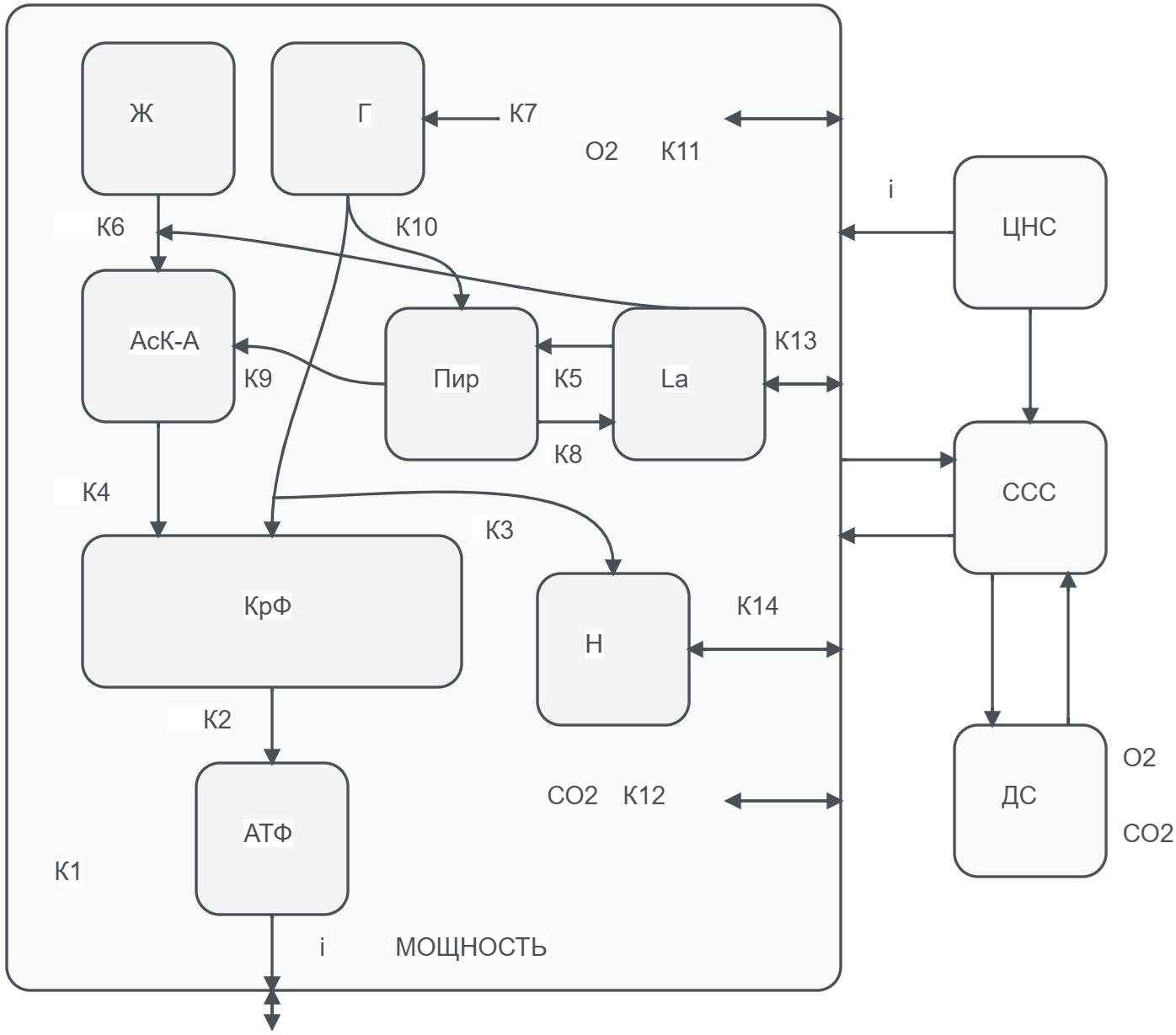
Relevance. The development of a comprehensive mathematical theory of athletic training continues to be a significant challenge in the field of sports science. Viktor Nikolaevich Seluyanov’s approach, based on compartment modeling, is a unique attempt to understand adaptation processes at all levels of the body, from cellular to systemic. Despite the potential for prediction, his models have not been widely adopted and require further analysis. The objectives are to systematize, reconstruct, and critically analyze the hierarchical system of mathematical models for short-term and long-term adaptation to training loads, developed by V.N. Seluyanov, and to assess their internal consistency, predictive power, and applicability. Methods. The study is based on the analysis and reconstruction of mathematical models derived from Seluyanov’s work. Systems of ordinary differential equations that describe shortterm and long-term adaptations, such as muscle bioenergetics and gas transport, as well as endocrine, immune, and digestive systems, have been reconstructed. Numerical modeling was performed using MATLAB and solvers for stiff systems. Results. The hierarchy of Seluyanov’s models has been organized. The short-term adaptation model accurately reproduces key physiological responses to exercise, such as the dynamics of creatine phosphate and ATP levels, lactate accumulation, and changes in cardiovascular and respiratory parameters. The long-term adaptation model shows the nonlinear dynamics of muscle fiber and mitochondrial growth, as well as how hormonal and immune status influence structural changes. It is shown that training at 70% of maximum capacity primarily stimulates muscle strength rather than aerobic fitness. Conclusions. The theoretical approach of V.N. Seluyanov represents an internally consistent mathematical theory of adaptation in sports, with significant predictive and educational potential. Reconstructed models enable a transition from empirical training planning to forecasting through simulation modeling. However, there are several limitations, such as the large number of empirical coefficients that require individual calibration, and a number of simplified assumptions. Despite these limitations, this approach continues to be relevant for the development of personalized training programs and decision support systems in elite sports.
mathematical modeling, athletic training, adaptation, compartmental models, differential equations, muscle bioenergetics, long-term adaptation, myofibrils, mitochondria, simulation modeling
1. Timme E. A. Towards a mathematical theory of athletic training. Part 1. The mathematical model of the training process and the equation of athletic performance by Nikolai Nikolaevich Engwer // Russian Journal of Information Technology in Sports. 2025. no. 2. pp. 24-41. DOI: https://doi.org/10.62105/2949-6349-2025-2-2-24-41 EDN: https://elibrary.ru/qkhjkj
2. Seluyanov V.N., Myakinchenko E.B., Gavrilov V.B., Rybakov V.A., Zaborova V.A., Kalinin E.M., Zimirev N.V., Kabanin D.N. Sports adaptology. Physical training in cyclic sports, Moscow, TVT Division, 2021, 524 p. (In Russ.)
3. Seluyanov V.N. Methods of building physical training of highly qualified athletes based on simulation modeling. Abstract of the dissertation... Doctors of Pedagogical Sciences : 13.00.04, Moscow, 1992, 47 p. (in Russ.) EDN: https://elibrary.ru/zllhaf
4. Seluyanov V.N. Methods of building physical training of highly qualified athletes based on simulation modeling. Dissertation... Doctors of Pedagogical Sciences : 13.00.04, Moscow, 1992, 318 p. (in Russ.)
5. Seluyanov V.N. Modeling in the theory of sports (physical training of athletes): A textbook for graduate students and students of SCOLIPE, Moscow, SCOLIPE, 1991, 58 p. (in Russ.) URL: https://rusneb.ru/catalog/010003_000061_914eeae5ee81cd21e995ad26bdb14d3e/
6. Seluyanov V.N., Myakinchenko E.B., Turaev V.T., Obukhov S.M., Kosmina I.P., Zubkova A.V., Bezdenezhnykh A.I. Theory and practice of applying didactics of developmental education in the training of physical education specialists. The works of the staff of the problematic research laboratory, Moscow, Physical Culture, Education and Science, 1996, 106 p. (in Russ.) ISBN 5-89022-040-3. URL: http://lib.sportedu.ru/Texts.idc?DocID=79706
7. Central Branch Library for Physical Culture and Sports. URL: https://gtsolifk.ru/obrazovanie/sportbiblioteka
8. Central Branch Library for Physical Culture and Sports (electronic catalog). URL: http://lib.sportedu.ru/
9. The laboratory of Professor Seluyanov. URL: https://vk.com/wall-98165439_2643
10. Marchuk G.I. Mathematical models in immunology, Moscow, Nauka Publ., 1980, 264 p. (in Russ.) URL: https://rusneb.ru/catalog/000200_000018_rc_1145984/
11. Novoseltsev V.N. Theory of control and biosystems. Analysis of preservation properties, Moscow: Nauka Publ., 1978, 320 p. (in Russ.) URL: https://www.nehudlit.ru/books/detail7231.html
12. Novoseltsev V.N. The organism in the world of technology. Cybernetic aspect, Moscow: Nauka Publ., 1989, 240 p. (in Russ.) URL: https://www.ipu.ru/node/65072
13. Margaria R. Biomechanics and energetics of muscular exercise. - Oxford University Press, Oxford, 1976, 346 p.
14. Morton R.H. On a model of human bioenergetics. European journal of applied physiology and occupational physiology, 1985, 54(3), pp. 285-290. URL: https://link.springer.com/article/10.1007/BF00426146
15. Morton R.H. On a model of human bioenergetics II: Maximal power and endurance. European journal of applied physiology and occupational physiology, 1986, 55(4), pp. 413-418. URL: https://link.springer.com/article/10.1007/BF00422743
16. Utkin V.L. Simulation of human motor activity: a textbook on biomechanics and sports metrology for students of the Higher School of Coaches, faculties of advanced training and advanced training, Moscow, SCOLIPE, 1983, 80 p. (in Russ.) URL: https://rusneb.ru/catalog/000199_000009_001181093/
17. Hunt B.R., Lipsman R.L., Osborn J.E., Rosenberg J.M. Differential Equations with MatLAB. 3rd Edition. — John Wiley & Sons, Inc., 2019. 296 p. ISBN: 978-1-118-37680-5 URL: https://www.mathworks.com/academia/books/differential-equations-with-matlab-hunt.html
18. A repository of code for mathematical models of human body adaptation to training effects. URL: https://gitverse.ru/Eger/Math_Models_Training_Performance
19. Novoseltsev V.N. Advantages and disadvantages of mathematical modeling. Fundamental Research, 2004, (6), pp. 121-122. (in Russ.) EDN: https://elibrary.ru/iumgqr