Москва, Россия
ВАК 1.5.5 Физиология человека и животных
ВАК 1.5.8 Математическая биология, биоинформатика
ВАК 5.8.4 Физическая культура и профессиональная физическая подготовка
ВАК 5.8.5 Теория и методика спорта
ВАК 5.6.6 История науки и техники
УДК 796.015 Спортивная тренировка. Методика. Нагрузка. Спортивные результаты
УДК 796.058.2 Анализ тренировки
ГРНТИ 77.00 ФИЗИЧЕСКАЯ КУЛЬТУРА И СПОРТ
ГРНТИ 20.00 ИНФОРМАТИКА
ОКСО 02.00.00 Компьютерные и информационные науки
ОКСО 06.00.00 Биологические науки
ББК 1 ОБЩЕЕ И МЕЖДИСЦИПЛИНАРНОЕ ЗНАНИЕ
ББК 22 Физико-математические науки
ББК 28 Биологические науки
ББК 75 Физическая культура и спорт
BISAC COM072000 Computer Simulation
BISAC COM017000 Cybernetics
BISAC COM062000 Data Modeling & Design
BISAC COM089000 Data Visualization
BISAC SPO047000 Training
BISAC BIO016000 Sports
BISAC MAT007010 Differential Equations / Ordinary
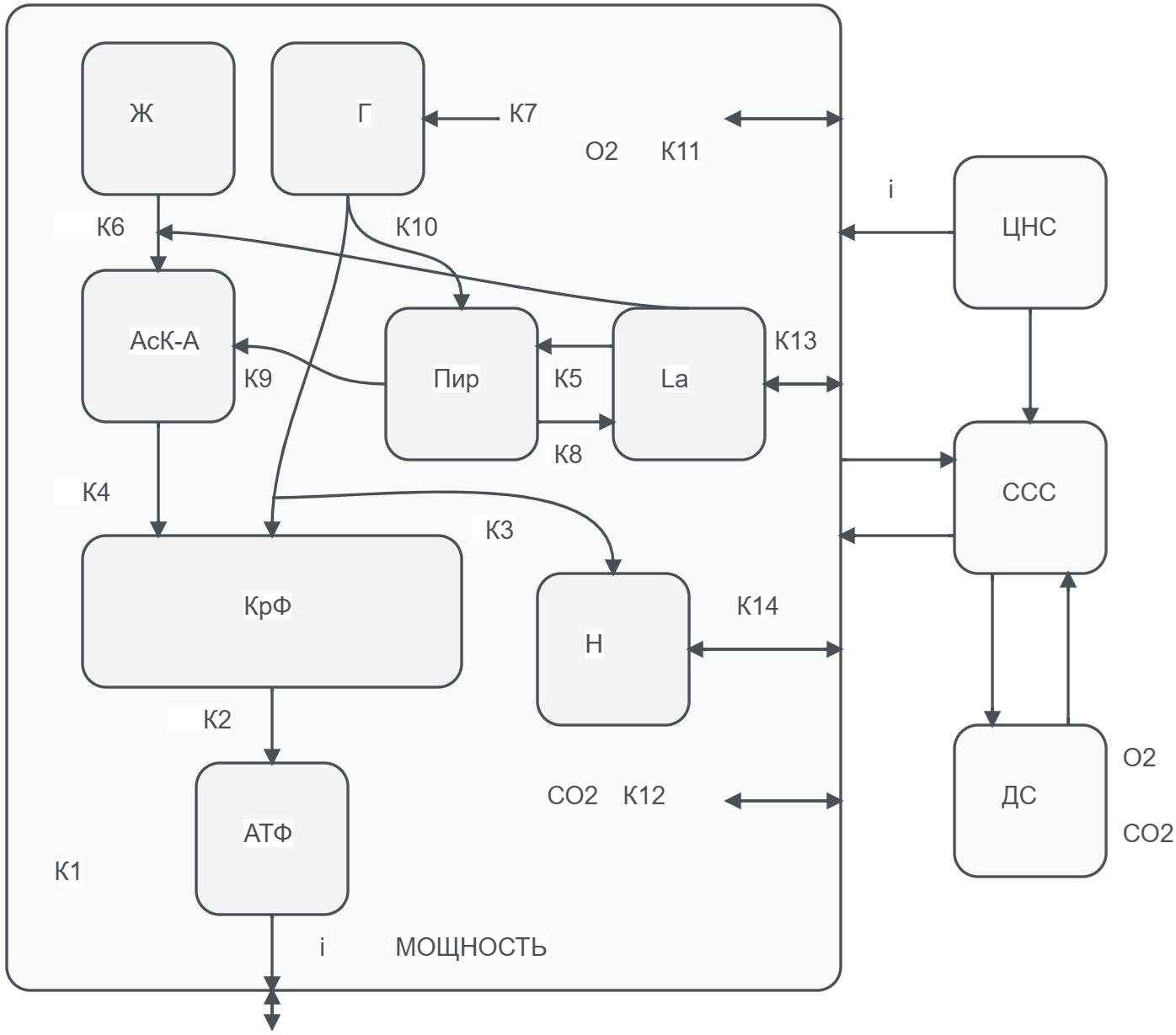
Актуальность. Создание целостной математической теории спортивной тренировки остается актуальной задачей спортивной науки. Подход Виктора Николаевича Селуянова, основанный на компартментальном моделировании, представляет собой уникальную попытку описания адаптационных процессов на всех уровнях организма — от клеточного до системного. Несмотря на прогностический потенциал, его комплексные модели не получили широкого распространения и требуют систематического анализа. Цель систематизировать, восстановить и критически проанализировать иерархическую систему математических моделей краткосрочной и долгосрочной адаптации к тренировочным нагрузкам, разработанную В.Н. Селуяновым, оценив их внутреннюю согласованность, предсказательную способность и области применения. Методы. Исследование основано на анализе и реконструкции математических моделей из работ В.Н. Селуянова. Восстановлены системы обыкновенных дифференциальных уравнений, описывающих краткосрочную адаптацию (биоэнергетика мышцы, транспорт газов) и долгосрочную адаптацию (эндокринная, иммунная, мышечная, пищеварительная системы). Численное моделирование выполнено в среде MATLAB с использованием решателей для жестких систем. Результаты. В работе систематизирована иерархия моделей Селуянова. Модель краткосрочной адаптации качественно воспроизводит ключевые физиологические реакции на нагрузку: динамику креатинфосфата и АТФ, накопление лактата, изменения сердечно-сосудистых и дыхательных показателей. Модель долгосрочной адаптации демонстрирует нелинейную динамику роста миофибрилл и митохондрий, а также влияние гормонального и иммунного статуса на структурные изменения. Показано, что режим нагрузки 70% от максимальной преимущественно стимулирует силовую, а не аэробную адаптацию. Заключение. Теоретический подход В.Н. Селуянова представляет собой внутренне непротиворечивую математическую теорию адаптации в спорте, обладающую значительным прогностическим и образовательным потенциалом. Восстановленные модели позволяют перейти от эмпирического планирования тренировок к прогнозу на основе имитационного моделирования. Основные ограничения связаны с большим количеством эмпирических коэффициентов, требующих индивидуальной калибровки, и рядом упрощающих допущений. Тем не менее, данный подход сохраняет актуальность для разработки персонализированных тренировочных программ и систем поддержки принятия решений в спорте высших достижений.
математическое моделирование, спортивная тренировка, адаптация, компартментальные модели, дифференциальные уравнения, биоэнергетика мышцы, долговременная адаптация, миофибриллы, митохондрии, имитационное моделирование
1. Тимме Е.А. На пути к математической теории спортивной тренировки. Часть 1. Математическая модель тренировочного процесса и уравнение спортивного результата Николая Николаевича Энгвера // Российский журнал информационных технологий в спорте. 2025. № 2. С. 24-41. DOI: https://doi.org/10.62105/2949-6349-2025-2-2-24-41 EDN: https://elibrary.ru/qkhjkj
2. Селуянов В.Н., Мякинченко Е.Б., Гаврилов В.Б., Рыбаков В.А., Заборова В.А., Калинин Е.М., Зимирев Н.В., Кабанен Д.Н. Спортивная адаптология. Физическая подготовка в циклических видах спорта. Москва: ТВТ Дивизион. 2021. 524 с. ISBN 978-5-98724-138-7
3. Селуянов В.Н. Методы построения физической подготовки спортсменов высокой квалификации на основе имитационного моделирования : автореферат дисc. ... д-ра пед. наук : 13.00.04. — Москва, 1992. 47 с. EDN: https://elibrary.ru/zllhaf
4. Селуянов В.Н. Методы построения физической подготовки спортсменов высокой квалификации на основе имитационного моделирования : дисс. ... д-ра пед. наук : 13.00.04. — Москва, 1992. 318 с.
5. Селуянов В.Н. Моделирование в теории спорта (физическая подготовка спортсменов): Учебное пособие для аспирантов и студентов ГЦОЛИФК. Москва: ГЦОЛИФК. 1991. 58 с. URL: https://rusneb.ru/catalog/010003_000061_914eeae5ee81cd21e995ad26bdb14d3e/
6. Селуянов В.Н., Мякинченко Е.Б., Тураев В.Т., Обухов С.М., Космина И.П., Зубкова А.В., Безденежных А.И. Теория и практика применения дидактики развивающего обучения в подготовке специалистов по физическому воспитанию: Труды сотрудников проблемной научно-исследовательской лаборатории / Научный руководитель В.Н. Селуянов. - Москва: Физкультура, образование и наука, 1996. 106 с. ISBN 5-89022-040-3. URL: http://lib.sportedu.ru/Texts.idc?DocID=79706
7. Центральная отраслевая библиотека по физической культуре и спорту. URL: https://gtsolifk.ru/obrazovanie/sportbiblioteka
8. Центральная отраслевая библиотека по физической культуре и спорту (электронный каталог). URL: http://lib.sportedu.ru/
9. Лаборатория профессора Селуянова. URL: https://vk.com/wall-98165439_2643
10. Марчук Г.И. Математические модели в иммунологии. Москва : Наука, 1980. 264 с. URL: https://rusneb.ru/catalog/000200_000018_rc_1145984/
11. Новосельцев В.Н. Теория управления и биосистемы. Анализ сохранительных свойств. М.: Наука, 1978. – 320 с. URL: https://www.nehudlit.ru/books/detail7231.html
12. Новосельцев В.Н. Организм в мире техники. Кибернетический аспект. М.: Наука, 1989. – 240 с. URL: https://www.ipu.ru/node/65072
13. Margaria R. Biomechanics and energetics of muscular exercise. - Oxford University Press, Oxford, 1976, 346 p.
14. Morton R.H. On a model of human bioenergetics. European journal of applied physiology and occupational physiology, 1985, 54(3), pp. 285-290. URL: https://link.springer.com/article/10.1007/BF00426146
15. Morton R.H. On a model of human bioenergetics II: Maximal power and endurance. European journal of applied physiology and occupational physiology, 1986, 55(4), pp. 413-418. URL: https://link.springer.com/article/10.1007/BF00422743
16. Уткин В.Л. Имитационное моделирование двигательной деятельности человека: учебное пособие по биомеханике и спортивной метрологии для слушателей Высшей школы тренеров, факультетов усовершенствования и повышения квалификации. Москва: ГЦОЛИФК, 1983. 80 с. URL: https://rusneb.ru/catalog/000199_000009_001181093/
17. Hunt B.R., Lipsman R.L., Osborn J.E., Rosenberg J.M. Differential Equations with MatLAB. 3rd Edition. — John Wiley & Sons, Inc., 2019. 296 p. ISBN: 978-1-118-37680-5 URL: https://www.mathworks.com/academia/books/differential-equations-with-matlab-hunt.html
18. Репозиторий кода математических моделей адаптации организма человека к тренировочным воздействиям. URL: https://gitverse.ru/Eger/Math_Models_Training_Performance
19. Новосельцев В.Н. Достоинства и недостатки математического моделирования //Фундаментальные исследования. 2004. № 6. С. 121-122. EDN: https://elibrary.ru/iumgqr